Clover - Arrow Trajectory Algorithm
I came up with the design of Clover after watching a bunch of game design videos by Masahiro Sakurai on youtube.
He mentions game essence which has to do with the push and pull of a game - whether a game rewards you for taking more risk.
When designing Clover, I decided to give the player a huge bonus for making combo kills. This would require that the player allows more enemies to get closer to them; increasing risk to the player.
After doing a bunch of hand-drawn sketches about possible layouts, I came to the conclusion that having a hero being chased by bandits on a cart would provide a good balance of realism weighed up against the gameplay I wanted.
Shooting a bow
Early versions of the game had the hero aiming directly at the mouse cursor. The more the bow was pulled, then the straighter the shot, but the arrow would always shoot under the mouse.
In a way this made shooting the bow feel pretty natural; you would learn to aim a little higher. The gameplay looked a little like this:

Showing the trail
Because the game was a fast-paced balance of risk and reward, I wanted to help the player see where they were aiming. So I added some circles to show the trajectory.
Calculating the trajectory is simple, an arrow moves with an initial speed and direction. There is no drag, and the arrow is pulled by gravity:
\[\begin{align} x(t) &= x(t_0) + \dot{x}(t_0)t \\ y(t) &= y(t_0) + \dot{y}(t_0)t + \frac{1}{2}gt^2 \\ \end{align}\]This looks like this:
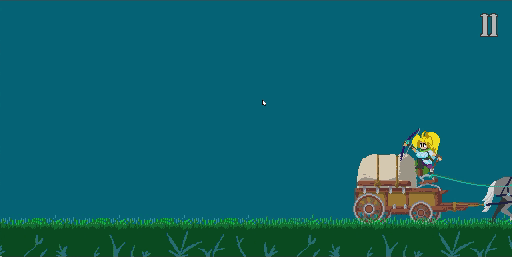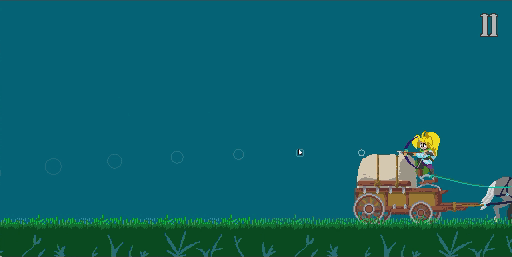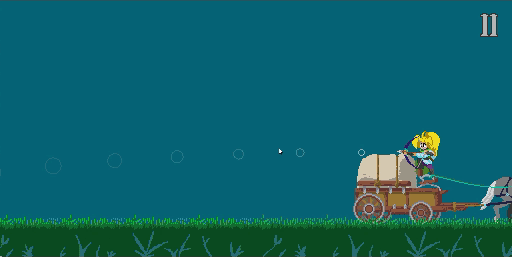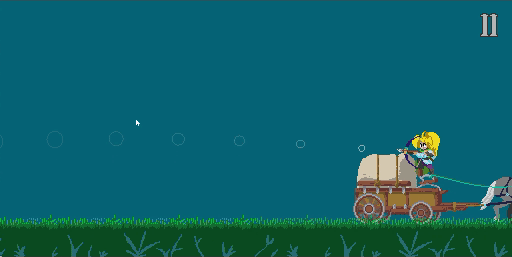
Unfortunately, it made the experience of shooting the bow. The trajectory was always under the mouse - it felt strange that your eyes were being drawn away from where you were pointing.
Solving for trajectory
I decided that I would prefer that the trajectory always tries to intercept the mouse.
This resulted in a new problem, how do I calculate the bow angle to make the arrow path intercept the mouse location?
Our equations of motion are:
\[\begin{align} x(t) &= x(t_0) + \dot{x}(t_0)t \\ y(t) &= y(t_0) + \dot{y}(t_0)t + \frac{1}{2}gt^2 \\ \end{align}\]We also know our initial velocity based on how far back the hero has pulled the bow:
\[\begin{align} v(t_0) &= \sqrt{\dot{x}(t_0) + \dot{y}(t_0)} \\ \end{align}\]Defining the mouse intercept time as \(t_m\) and defining the distances to cover as \(\Delta{x}\) and \(\Delta{y}\):
\[\begin{align} \Delta{x} &= x(t_m) - x(t_0) \\ \Delta{y} &= y(t_m) - y(t_0) \\ \end{align}\]We rearrange our equations to a quadratic which solves for \(t_m^2\):
\[\begin{align} 0 &= {\Delta{x}}^2 + {\Delta{x}}^2 - \left( {v}^2(t_0) + \frac{1}{2}g\Delta{y} \right)t_m^2 + \frac{1}{4}g^2t_m^4 \\ \end{align}\]This can be solved using the quadratic formula:
\[\begin{align} z &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \\ \end{align}\]where:
\[\begin{align} z &= t_m^2 \\ a &= \frac{1}{4}g^2 \\ b &= - \left( {v}^2(t_0) + \frac{1}{2}g\Delta{y} \right) \\ c &= {\Delta{x}}^2 + {\Delta{x}}^2\\ \end{align}\]We can now solve for the angle:
\[\begin{align} \tan(\theta) &= \frac{\dot{y}(t_0)}{\dot{x}(t_0)}\\ \dot{x}(t_0) &= \frac{\Delta{x}}{t_m} \\ \dot{y}(t_0) &= \frac{\Delta{y} - \frac{1}{2}g{t_m}^2}{t_m} \\ \end{align}\]Giving:
\[\begin{align} \theta &= \tan{\frac{\Delta{y} - \frac{1}{2}g{t_m}^2}{\Delta{x}}} \end{align}\]The resulting algorithm has the trajectory go through the mouse position:

There may be a brief period where the arrow cannot intercept the mouse position; when this happens, we just point the bow towards the mouse.
If you want to play clover, you can check it out here:


