Hexagonal Game of Life

Last year, I took Mark Rober’s 30-day creative engineering course which emphasises the creative process from idea to build completion.

One of the builds was themed around art.

I had earlier been obsessed with some hexagonal shelves that I had found at the local hardware store, but I had no reason to buy them.

So to justify my impulsive consumerism I built a novel game-of-life on a hexagonal grid.

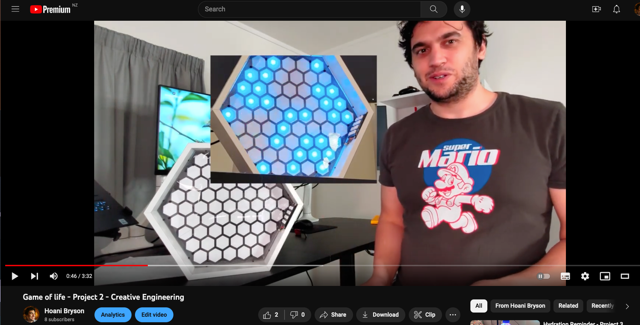
After completing the the chatbox and lazerpaw projects; I revisited this project to tidy it up and add an end-of-life detection algorithm.

Before	After

Rules of the Game

Hexagonal game of life is similar to a square grid game of life.

The major difference is that instead of a cell having 9 neighbours, it will typically have 6.

The exceptions are the corner cells with 3 neighbours and the edge cells with four.

We always start the game with each cell assigned either alive or dead randomly.

Then for each step of the game we apply the following rules, where n is the number of living neighbours a cell has:

• For dead cells:
  • If n == 2 or n == 3, life begins in your cell
• For living cells
  • If n < 2, life ends due to loneliness
  • If n > 3, life ends due to overpopulation

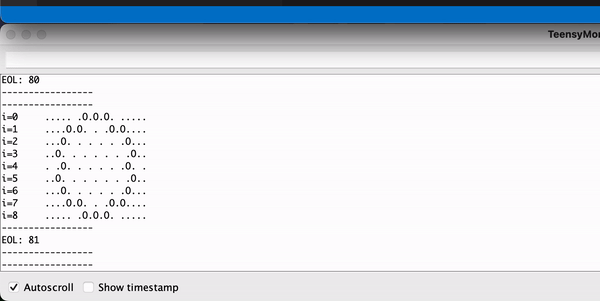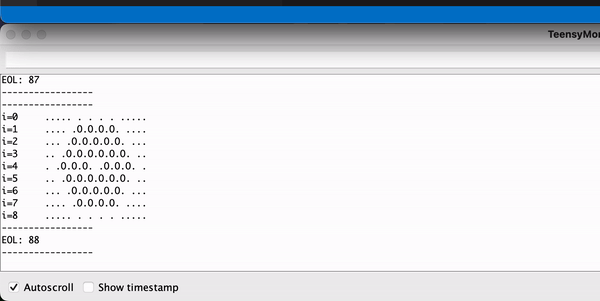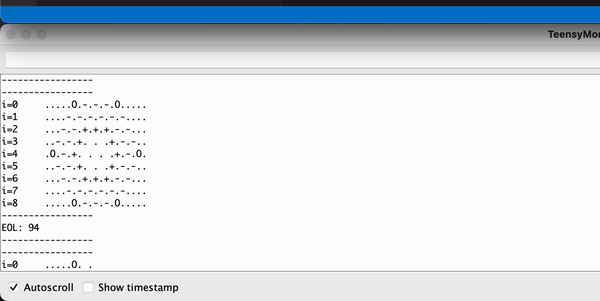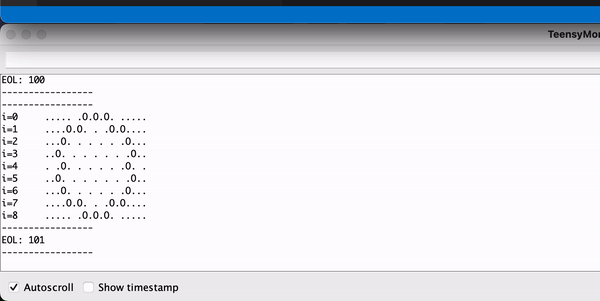
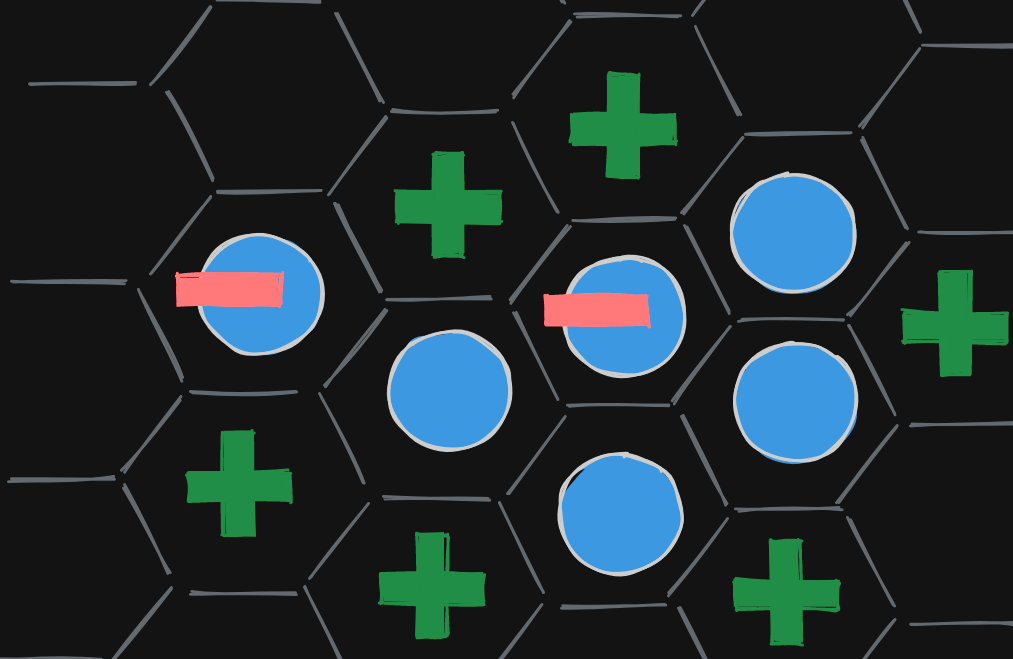
This image illustrates these rules, where we have two living cells about to die due to lonliness or overpopulation:

The game of life can get stuck in a looping pattern.

Because each step is completely deterministic, the game will never exit the loop.

I added a final rule to keep the build always doing interesting things:

• Once the game gets stuck in a loop, it ends and restarts.

Detecting End of Life

To enforce the last rule, we need an algorithm to detect it is stuck in a loop. I called this the End of Life (EoL) algorithm.

Because this is running on embedded hardware, I wanted the detection to be lightweight and not require too much processing power.

The End of Life algorithm is:

• On each step, calculate a uint64_t entry value which represents the current board.
  • There are 61 cells, so the entry value uses 61 of it’s bits to represent the state of the board.
• We store 16 entry values in an eolEntries array:
  • Value 0 is stored on each game step
  • Value 1 is stored on every 2nd game step
  • Value 2 is stored on every 4th game step
  • Values 3 to 16 is stored on every 2^nth game step
• On each step, we check if the current entry matches any of the previous values in eolEntries
• If it does, the End of Life sequence begins so that the game will restart.

The benefits of this algorithm is:

• can detect loops up to 65536 steps long
• uses only 128 bytes of RAM
• computationaly deterministic and light
  • only requires around 500 operations per step
• at most a loop can only repeat twice before it is detected

I wanted the End of Life sequence to be a special part of the game. So once End of Life is detected, I trigged a speaker to play Final Voyage from Outer Wilds. As this happens, the game continues with the cells slowly turning white. At the end of the song, cells stop dying until the entire board fills up, and then all die at once.

Build Details

Hardware

The hardware in this project includes:

• WS2812 LED strips
• Teensy 4.0
• PJRC’s Audio Adaptor shield
• 5V (3A) power supply
• A 5V Speaker with Audio jack input
• Enclosure
  • Hexagonal shelf
  • 3D printed parts
  • White plastic for diffusing the LEDs

Software

The software was written in C++ using arduino.

Check it out at github.com/hoani/hex-game-of-life

Debugging

To help debug the project, I added a serial_view which allows us to see the game of life on a serial terminal window.